Strengthen math visualization skills using bar model drawing techniques effectively
Wiki Article
Exploring Bar Model Drawing Techniques: A Comprehensive Guide to Visualizing Math Concepts
Bar model drawing methods serve as a useful resource for both instructors and trainees in envisioning mathematical principles. These designs streamline complex mathematical relationships, helping in the understanding of enhancement, subtraction, division, and reproduction. This guide describes efficient strategies for executing bar versions, fostering energetic involvement and real-world links. As readers explore the useful applications and teaching ideas, they will certainly uncover how these strategies can change their strategy to mathematics.Comprehending the Fundamentals of Bar Design Illustration
Bar version attracting works as a powerful aesthetic device in maths, facilitating the understanding of analytical strategies and numerical connections. This strategy entails representing numbers and their relationships via rectangular bars, making it simpler to imagine operations such as enhancement, division, reproduction, and reduction. Each bar's length represents a certain value, enabling students to compare amounts and recognize proportions plainly.To create a bar model, one starts by determining the problem's essential components, commonly damaging it down right into parts that can be aesthetically represented. In a straightforward addition trouble, 2 bars can be drawn, with their lengths representing the addends. The mixed length highlights the amount. Furthermore, bar models can be adapted for more complicated issues, including portions and ratios, by readjusting the bars appropriately. Grasping these fundamentals lays a solid foundation for effective problem-solving and deeper mathematical comprehension.
Benefits of Utilizing Bar Models in Mathematics
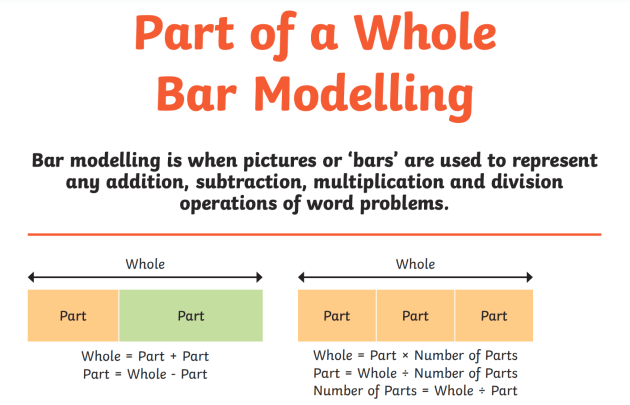
Utilizing bar models in mathematics uses numerous advantages that boost learning and understanding. These aesthetic depictions help pupils in grasping complicated ideas by breaking them down right into convenient components. Bar versions offer a clear framework for showing connections in between numbers, making abstract concepts much more concrete. They advertise a deeper understanding of mathematical operations and assist in problem-solving by permitting learners to envision the information they are dealing with.Bar designs support the development of crucial thinking skills, as trainees need to assess and analyze the visual details to attract conclusions. This method urges active engagement with the product, enhancing retention and mastery of mathematical principles. By promoting a strong structure in aesthetic proficiency, bar designs encourage students to come close to different mathematical obstacles with self-confidence. In general, the combination of bar designs right into mathematics education shows advantageous in cultivating both comprehension and analytical capacities amongst pupils.
Using Bar Models to Addition and Reduction
Bar versions function as a reliable device for visually standing for enhancement and subtraction problems. By highlighting the partnership between numbers, they improve understanding and help with problem-solving. Furthermore, real-life applications of these models can aid learners understand mathematical ideas in functional contexts.Representing Enhancement Aesthetically
When students encounter enhancement and reduction issues, visual help can greatly enhance their understanding of these procedures. Bar models work as efficient devices for standing for enhancement. By separating a rectangle right into segments that match to the numbers involved, trainees can imagine the relationship between the amounts. If a student requires to include 3 and 5, they can produce a bar split right into 2 areas: one section representing 3 and the other standing for 5. This clear representation not just simplifies the enhancement process yet additionally reinforces the principle of combining quantities. As students manipulate these visual aids, they establish a deeper comprehension of addition, leading to enhanced problem-solving skills and higher confidence in their mathematical capacities.
Reduction With Bar Versions
Reduction is often perceived as an extra intricate procedure than enhancement, bar versions can efficiently clarify this procedure for pupils. By aesthetically standing for the amounts involved, students can better understand just how numbers associate with one another. In a bar model for reduction, one bar stands for the total amount, while an additional shows the amount being deducted. This aesthetic distinction helps students comprehend the idea of "taking away." For example, if a bar shows 10 units, and one more bar standing for 4 units is eliminated, trainees can easily see that 6 units remain. This strategy not just cultivates understanding of reduction but also help in creating analytic skills, allowing students to imagine their mathematical reasoning and boost their overall understanding of mathematical concepts.Real-Life Application Examples
Understanding reduction through bar designs lays a foundation for using these methods in real-life situations. In different contexts, such as budgeting or shopping, people can imagine how much cash stays after expenses. If a person has $50 and invests $20, a bar model can stand for the total amount and the spent portion, illustrating that $30 is left. Furthermore, parents can utilize bar designs to help kids understand just how lots of more products require to be included in finish a set, such as having three apples and requiring 5. This aesthetic depiction simplifies intricate issues, promoting comprehension and retention. Ultimately, bar models act as reliable tools in daily decision-making, boosting mathematical understanding in useful situations.Picturing Reproduction and Division With Bar Versions
In discovering the application of bar models for reproduction and department, it is necessary to comprehend their fundamental concepts. Building reproduction designs permits students to envision connections between numbers, while effective division approaches can be illustrated via these visual aids. This strategy enhances comprehension and analytical abilities in mathematics.Understanding Bar Designs
Bar designs act as an effective aesthetic device for highlighting the principles of reproduction and department. They make it possible for students to represent mathematical relationships in a structured format, assisting in a much deeper understanding of these procedures. In reproduction, bar designs display teams of equivalent dimension, permitting people to picture the overall amount when integrating these groups. On the other hand, in division, bar designs aid portray how a total is divided right into smaller sized, equivalent parts, clarifying the principle of dividing. By utilizing these visual aids, students browse this site can grasp the underlying concepts of reproduction and division better. This method not just boosts comprehension but additionally sustains analytical skills, making bar models an invaluable asset in mathematical education and learning.Building Reproduction Versions
Constructing reproduction designs using bar diagrams supplies a clear technique for visualizing the procedure of reproduction. These models enable learners to represent reproduction as groups of equivalent parts, making abstract principles much more concrete. For instance, to show (3 times 4), a trainee can draw one bar split right into three equal sectors, each representing 4 devices. In addition, producing a 2nd bar with the exact same size reinforces the understanding of duplicated addition, as each sector corresponds to one team. This graph not just help in realizing reproduction yet likewise boosts analytical skills. By using bar models, trainees can much better comprehend connections Source in between numbers and create a robust foundation for a lot more complex mathematical concepts, bring about enhanced confidence in their abilities.Visualizing Division Methods
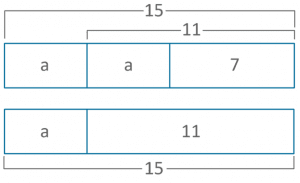
Addressing Word Problems Making Use Of Bar Design Techniques

As an example, in a problem entailing addition and subtraction, trainees can draw separate bars for each quantity and after that manipulate them to find the option. This process not only clarifies the problem but additionally promotes a deeper theoretical understanding. Furthermore, bar versions can be adjusted for various sorts of word troubles, making them functional throughout different mathematical topics. Inevitably, utilizing bar models can significantly improve trainees' problem-solving abilities by offering a clear aesthetic path to get to the correct solution.
Integrating Bar Versions in Various Math Topics
Bar versions can be effortlessly integrated right into numerous mathematics topics, enhancing pupils' understanding of ideas beyond standard arithmetic. In algebra, these aesthetic tools help in representing inequalities and equations, making it possible for learners to picture connections in between variables. When taking on geometry, bar designs can illustrate the residential or commercial properties of forms and spatial reasoning, assisting students realize principles like location and border successfully. In data, bar models assist in the interpretation of data collections, permitting pupils to compare amounts and identify trends aesthetically. Furthermore, incorporating bar versions within measurement subjects aids in comprehending devices and conversions by providing a concrete depiction of quantities. By utilizing bar designs throughout various mathematical areas, teachers can promote a much deeper comprehension of intricate concepts, thus enhancing analytic skills and promoting essential reasoning (bar model drawing techniques). This convenience demonstrates the utility of bar designs as a foundational tool for trainees in their view it now mathematical tripTips for Training Bar Versions Properly
Incorporating bar models right into teaching practices requires thoughtful approaches to maximize their efficiency. Educators must start by introducing bar models with straightforward, relatable instances that pupils can conveniently realize. This aids to construct self-confidence and familiarity with the concept. Gradually increasing the intricacy of issues permits students to apply their skills considerably. Additionally, teachers need to urge trainees to develop their very own bar models, promoting energetic involvement and possession of their understanding.Including collective activities can also boost understanding, as pupils talk about and resolve troubles in teams. Constant feedback is essential; educators ought to provide positive commentary on students' bar version depictions to assist renovation. Connecting bar versions to real-life circumstances enhances their significance, helping pupils see the useful applications of their mathematical abilities. By implementing these approaches, teachers can properly harness the power of bar designs in their maths instruction.
Often Asked Inquiries
Can Prevent Designs Be Used in Other Topics Besides Math?
Bar versions can certainly be made use of in various topics beyond mathematics. They effectively show principles in science, social researches, and language arts, helping to visually stand for partnerships, processes, and concepts for enhanced understanding across self-controls.What Age Group Is Finest Matched for Learning Bar Designs?
Bar models are best fit for children ages 7 to 12, as they establish concrete reasoning abilities during this period (bar model drawing techniques). At this age, pupils can properly grasp abstract principles with aesthetic depiction and problem-solving methodsExist Digital Devices for Creating Bar Versions?
How Can I Examine Student Recognizing of Bar Designs?
Examining pupil understanding of bar versions can involve tests, observational analyses, and team conversations. Educators could likewise analyze pupils' finished designs and their ability to describe their reasoning, ensuring an extensive examination of comprehension.What Prevail Mistakes When Making Use Of Bar Versions?
Typical errors when utilizing bar versions include misrepresenting quantities, failing to accurately label bars, confusing enhancement and subtraction, ignoring to use constant ranges, and ignoring the importance of clear aesthetic separation between various aspects.In addition, bar designs can be adjusted for more intricate problems, including portions and proportions, by readjusting the bars as necessary. Subtraction is typically perceived as a much more intricate procedure than addition, bar models can successfully clarify this process for pupils. In a bar design for subtraction, one bar represents the overall, while an additional shows the quantity being deducted. If a bar reveals 10 devices, and another bar representing 4 devices is removed, trainees can quickly see that 6 systems remain. When dividing an overall right into equivalent teams, students can draw a long bar to represent the whole and after that sector it right into smaller sized bars that indicate each group.
Report this wiki page